Einführung in die Schwarmintelligenz
Der Aufstieg der künstlichen Intelligenz durch neuronale Netze hat das 21. Jahrhundert geprägt. Dieser Blogbeitrag erkundet ein weiteres faszinierendes Gebiet, Schwarmintelligenz. Inspiriert von biologischen Phänomenen, entfaltet sie kollektive Intelligenz. Wir tauchen ein in die Grundlagen, erkunden faszinierende Beispiele wie Ameisen auf Futtersuche und entdecken Algorithmen wie den Ameisenalgorithmus und die Partikelschwarmoptimierung. Tauche ein und entdecke das Potenzial!
Schwarmintelligenz
1 Einleitung
1.1 Motivation für Schwarmintelligenz
Das 21. Jahrhundert ist maßgeblich durch Daten und künstlicher Intelligenz geprägt. Der große Aufschwung des Gebiets ist auf künstliche Neuronale Netze (NN) zurückzuführen. Dieses Verfahren ermöglicht es, komplexe Zusammenhänge zu erlernen, an denen "traditionelle" Verfahren gescheitert sind. Als Vorbild für NN dienten die Neuronen und ihre Vernetzung im biologischen Gehirn eines Lebewesens.1 NN sind ein erfolgreiches Beispiel für einen Transfer aus der Biologie in die Informatik, dennoch gibt es auch weitere Forschungsgebiete aus der Biologie, die der Informatik als Vorbild dienen, viel Potential besitzen und die Gesellschaft ebenso prägen können wie NN.
Eines dieser weiteren Anwendungsgebiete, bei dem sich die Informatik Konzepte aus der Biologie abschaut, ist die Schwarmintelligenz (auch Kollektive Intelligenz genannt). Schwarmintelligenz beschreibt ein emergentes Phänomen, bei dem eine Intelligenz durch den Zusammenschluss und das Zusammenwirken von vielen Individuen erreicht wird.2
1.2 Zielsetzung
Ziel dieses Blogbeitrags ist es, die Grundlagen von Schwarmintelligenz zu beschreiben. Dafür wird zunächst ein Vorbild aus der Biologie für die technische Umsetzung von Schwarmintelligenz beschrieben. Aus dem Vorbildern sollen dann die wesentlichen Kernideen und -konzepte, die für die Informatik von Interesse sind, identifiziert werden. Anschließend werden zwei klassische Algorithmen aus dem Bereich der Schwarmintelligenz vorgestellt und beschrieben.
2 Grundlagen von Schwarmintelligenz
2.1 Schwarmintelligenz in der Biologie
Für manche Lebewesen, z.B. Fische und Vögel, ist es einfacher, im Schwarm zu agieren. Es hilft ihnen u.a. bei der Nahrungssuche und der schnelleren Fortpflanzung.3 Ameisen und Bienen bilden als Insekten im biologischen Sinne keinen Schwarm, sondern Kolonien, jedoch können Kolonien im Sinne der Schwarmintelligenz aus informationstechnischer Sicht mit Schwärmen gleichgesetzt und als solche betrachtet werden.4 Wie sich die Informatik das Verhalten von Ameisen zunutze macht, wird nachstehend beschrieben.
2.1.1 Ameisen auf Futtersuche
Ameisen gelten als bekanntes Beispiel für Schwarmintelligenz, da die gesamte Gruppe in der Lage ist, komplexe Aufgaben zu lösen. Da die meisten Futterquellen nicht in unmittelbarer Nähe des Nests zu finden sind, müssen sich Ameisenkolonien zur Nahrungsaufnahme auf Futtersuche begeben. Goss et al. hat das Verhalten von Ameisen auf Futtersuche untersucht und erste Konzepte in dem Vorgehen der Ameisen auf Futtersuche veröffentlicht.5 Dabei gehen Ameisen wie folgt vor: Zunächst werden ungeordnet einzelne Ameisen-Kundschafter entsandt, um nach Futterquellen zu suchen. Wurde eine Futterquelle identifiziert, kehrt die Ameise mit einer kleinen Futterprobe zurück zum Nest. Die Pheromone, (Duftstoffespur), die die Ameise hinterlässt, führen die anderen Ameisen zu dieser Futterquelle. Pheromonspuren verflüchten nach kurzer Zeit. Ameisen orientieren sich in der Regel nach den Weg mit der stärksten Pheromonspur. Wenn an einer Gabelung für die möglichen Wege keine Pheromonspuren existieren oder alle die gleiche Konzentration haben, wird ein zufälliger Weg gewählt. Zu Beginn werden alle Routen zur Futterstelle etwa gleich oft gewählt. Da aber Ameisen mit kurzen Wegen schneller zum Nest zurückkehren können, sind die vorhandene Geruchsspuren auf den kurzen Wegen intensiver. Die anderen Ameisen folgen nun dem geruchsintensiveren Weg und hinterlassen dadurch auch wieder Duftstoffe. Letztlich orientieren sich immer mehr Ameisen an der kürzeren Route, wodurch die Pheronomkonzentration so stark zunimmt, dass schließlich Umwege vermieden werden, da alle Ameisen den gleichen Weg einschlagen (Ameisenstraße). Durch ihr Kollektiv bilden die Ameisen ein komplexes Netzwerk und optimieren so ihre Futtersuche.
2.2 Schwarmintelligenz in der Informatik/Robotik
Neben dem oben genannten Beispiel gibt es in der realen Welt noch weitere Anwendungsfälle von Schwarmintelligenz in der Biologie. Die Grundideen und Konzepte aus der biologischen Schwarmintelligenz lassen sich auf folgende Teilgebiete der Schwarmintelligenz in der Informatik/Robotik transferieren:6
- Aggregation beschreibt das Ziel der Individuen, den Abstand zu seinen Nachbarn zu verringern. Jedes Objekt kennt dabei maximal nur die Positionen und Zustände seiner direkten Nachbarn.
- Dispersion beschreibt das Gegenteil von Aggregation und gibt den Objekten das Ziel, den Abstand zu seinen Nachbarn zu maximieren.
- Flocking beschreibt eine kollektive Bewegung von Objekten und wird typischerweise in der Animationstechnik zur Simulation von bspw. Vögeln in Videospielen eingesetzt.
- Sortieren
- Suche und Optimierung
- Kollektiver Transport
- Kollektives Bauen
- Kollektives Entscheiden
Wie bereits oben beschrieben, gibt es mehrere Beispiele aus der Biologie, in denen Schwarmintelligenzen vorkommen. Obwohl sich alle Einsatzgebiete unterscheiden lassen, können trotzdem Kernkonzepte identifiziert werden, die bei einem Transfer auf andere Problemstellungen beachtet werden sollten. Schmickl stellt folgende fünf Prinzipien auf:4
- Prinzip der Nachbarschaft
- Prinzip der Qualität
- Prinzip der verschiedenartigen Antwort
- Prinzip der Stabilität
- Prinzip der Anpassungsfähigkeit
In der Informatik wird jedes Individuum/Objekt als ein Agent repräsentiert. Ein Agent besitzt nach Bogon selbstorganisatorische folgende Fähigkeiten: autonom, proaktiv, reaktiv, robust, adaptiv, kognitiv, sozial.7
2.2.1 Ameisenalgorithmus
Der Ameisenalgorithmus (engl. Ant Colony Optimization (ACO)) beschreibt das Vorgehen der Ameisen auf Futtersuche, welches in Abschnitt 2.1.1 beschrieben wurde. Der Ameisenalgorithmus hilft dabei, das Optimum in kombinatorischen Problemen zu finden und kann bsw. das Problem des Handlungsreisenden (TSP) lösen. In diesem Problem soll ein Handlungsreisender bestimmte Städte besuchen und dabei in der gleichen Stadt auskommen, in der er gestartet ist. Im Folgenden wird der Algorithmus von Dorigo et al. vorgestellt.8
Grundsätzlich lässt sich die Problemstellung des Handlungsreisenden über einen Graphen darstellen, wobei die Knoten für bestimmte Positionen oder Orte stehen und durch Kanten verbunden werden können. Insgesamt existieren Knoten, und eine Kante verbindet die Orte und mit einer Gewichtung , die für die Entfernung steht. Die Kantengewichte werden in einer Kostenmatrix (engl. cost matrix) abgebildet.
Die Pheromone lassen sich ebenfalls in einer Matrix abbilden. Dabei gilt: Je höher der Wert, desto stärker ist die Pheromonkonzentration.
Im Fall des Handlungsreisenden bedeutet dies, dass er einen möglichst optimalen Weg ermittelt. Bezogen auf den Grundgedanken der Schwarmintelligenz gibt es aber nun Ameisen, die sich auf dem Graphen bewegen und Pheromone ausstoßen. Die Entscheidung der Ameise , die Kante ausgehend von ihrem aktuellen Knoten i hin zu j zu wählen, wird über die folgende Wahrscheinlichkeit ermittelt:
.
Dabei beschreibt die Pheromonkonzentration auf dieser Kante. ist das Maß, das die Sichbarkeit einer Kante beschreibt und wird über berechnet. ( ist der zugehörige Wert in der Kostenmatrix). Je geringer die Distanz einer Kante, desto größer ist die Sichtbarkeit. Ferner lässt eine geringe Sichtbarkeit nicht unbedingt auch eine kürzere Strecke für die gesamte Route schließen. Die Konstanten können verwendet werden, um den Einfluss der Pheromonkonzentrations und der Sichtbarkeit individuell anzupassen (Trade-off). Die Menge beinhalt alle Kanten, die von dem aktuellen Standort erreichbar sind und umfasst alle unbesuchten Knoten der Ameise . Die Summe summiert die Produkte der Sichtbarkeit und Pheromone für alle Kanten in , die von dem Knoten , auf der sich die Ameise aktuell befindet, erreichbar sind und bisher noch nicht besucht wurden.
Eine Iteration endet, nachdem alle Ameisen wieder zum Ausgangspunkt zurückgekehrt sind. Nach Abschluss einer Iteration werden die Pheromonwerte auf den Kanten aktualisiert. Außerdem sondert sondert jede Ameise nach einer Iteration ein bestimmte Menge an Pheromonen auf der besuchten Kante ab. Diese berechnet sich wie folgt:
Hat Ameise bereits die Kante besucht, gilt . Andernfalls wird auf Null gesetzt. Dabei ist eine Konstante, die einer geschätzten kürzesten Distanz für die Problemlösung entspricht und entspricht der bereits von Ameise zurückgelegten Distanz in der aktuellen Iteration.
Hat die Ameise eine Distanz zurückgelegt, die dem geschätzten Optimum nahe kommt oder übertrifft, werden auf den besuchten Kanten durch diese Ameise größere Pheromonwerte hinterlegt als bei einer Ameise, die in der gleichen Iteration eine längere und somit ineffizientere Route gewählt hat.
Für die Aktualisierung der Pheromonwerte muss zunächst die Summe aller neu hinterlegten Pheromone berechnet werden. Diese Summe berechnet sich wie folgt: .
Wie anhand des biologischen Vorbilds beschrieben, kann die Duftspur verflüchten. Diese Eigenschaft wird bei der Aktualisierung der Pheromonwerte für die Kanten berücksichtigt. Die neuen Pheromonwerte für Kante werden nach jeder abgeschlossenen Iteration wie folgt berechnet:
Dabei ist der Pheromonwert für die nächste Iteration und ist der Pheromon-Verdunstungskoeffizient (ein großer Koeffizient lässt die Pheromonwerte schnell verfliegen).
Die Auswahl der Populationsgröße der Ameisen hat einen großen Einfluss auf den Ablauf. Eine große Population kann zwar schneller eine optimale Lösung finden, ist aber zugleich rechenintensiver. Eine Möglichkeit ist (Knoten = Ameinsen). Grundsätzlich sollte, ähnlich wie in der Biologie, im Sinne einer Schwarmintelligenz zu einer größeren Menge tendiert werden.6 9
Mittlerweile haben sich weitere Algorithmen etabliert, die das oben beschriebene Vorgehen ergänzen und hinsichtlich Laufzeit und Ergebnisse verbessern.10
Für Internet of Things (IoT) wird der Ameisenalgorithmus bspw. dafür eingesetzt, eine optimale Route innerhalb einer denzentralen Netzwerkkommunikation zu finden.11 12
2.2.2 Partikelschwarmoptimierung
Der Begriff Partikelschwarmoptimierung (PSO) wurde von Kennedy et al. erstmals veröffentlicht und lässt sich ebenso wie der Ameisenalgorithmus bei den Optimierungsalgorithmen einordnen.13 Als Vorbild für PSO dient das Schwarmverhalten von Vögeln.
Das Ziel von PSO ist es, das Optimum (Maximum oder Minimum) einer Zielfunktion zu finden. Dabei durchsucht ein Schwarm bestehend aus Partikeln als Kollektiv den Suchraum. Die Position eines Partikels bestimmt die Qualität des aktuellen Standorts hinsichtlich des gesuchten Optimums und entspricht dem dazugehörigen Funktionswert von . Für den Ablauf des Algorithmus ist es notwendig, dass die Partikel untereinander kommunizieren können. Die Fortbewegung der Partikel hängt von der Geschwindigkeit und Richtung ab. Die Richtung und somit die neue Position setzt sich aus der aktuellen Richtung des Partikels, den Koordinaten des bisher individuellen Bestwerts und den Koordinaten des globalen Bestwerts zusammen (siehe Abbildung 2.1). Der globale Bestwert entspricht entweder dem aller Partikel oder dem seiner engsten Nachbarschaft. Floreano et al. empfehlen eine Schwarmgröße, die im Bereich von Partikeln liegt und eine Nachbarschaftspopulation, die etwa 10% der Gesamtmenge ausmacht.14
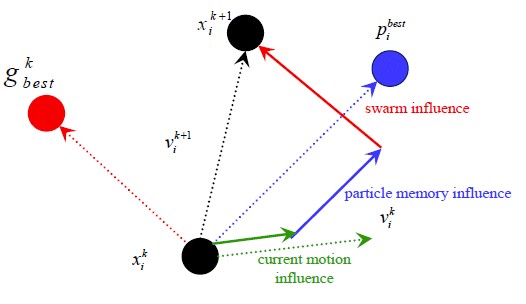
Abbildung 2.1: Die Bewegungsrichtung der Partikel hängt von drei Faktoren ab. Quelle: 14
Je nach Umsetzung kann der globale beste Wert entweder der beste Wert der aktuellen Iteration/Generation sein oder dem besten Wert aus allen bisher durchgeführten Iterationen entsprechen. Im Folgenden wird die erste Version beschrieben.
Nach jeder Iteration berechnet jedes Partikel seine neue Position auf der Grundlage der letzten (bzw. aktuellen) Position und der Geschwindigkeit (inkl. Richtung), um von der aktuellen Position zu der nächsten Position zu gelangen. Die Formel für die Positionsänderung sieht wie folgt aus:
Die Geschwindigkeit setzt sich aus den drei Richtungseinflüssen zusammen:
Dabei steht für die aktuelle Position des -ten Partikels in der -ten Iteration. Weiter steht für die Position des bisher besterzielten Werts innerhalb der Nachbarschaft des -ten Partikels. Die Zufallszahlen , gewährleisten eine zuästzliche Randomisierung und die Konstanten gewichten individuell die drei Richtungsflüsse.
2.2.2 Evolution
Der evolutionäre Gedanke der Biologie spielt ebenso in der Informatik/Robotik eine wichtige Rolle. Das Grundkonzept der genetischen Algorithmen sieht vor, in jeder Generation die besten Parametereinstellungen, Entscheidungsregeln, Lösungsmengen und/oder KI-Modelle zu übernehmen. Dabei können entweder die Lösungsmengen einzelner Agenten/Robotern berücksichtigt werden, falls diese mit unterschiedlichen Werten initalisiert worden sind oder die aggregierte Lösungsmenge der gesamten Gruppe, sofern alle Agenten mit gleichen Werten gestartet sind. Die beste Lösungsmenge überschreibt nicht direkt die der vorherigen Generation, sondern wird bspw. mit Hilfe einer Lernrate aktualisiert.15 16 7
3 Fazit
Schwarmintelligenz ist ein vielversprechendes Forschungsgebiet und bietet entsprechend großes Potential. Vor allem in der Robotik profitieren die Use Cases durch die Einfachheit der Agenten, die Skalierbarkeit, Ausfalltoleranz und Parallelität. Allerdings sollte man sich vor der Umsetzung überlegen, ob die Aufgabe nicht besser durch zentral gesteuerte Einheiten oder lediglich mittels eines Roboters gelöst werden kann, der aber so "intelligent" ist wie der Schwarm. Der Materialverbrauch in der Robotik und die daraus resultierenden Kosten bei einem Schwarm sind höher als bei einem singulären Agenten. Zudem stellt in der Praxis die Umstellung bzw. Anpassung der Schwärme auf minimal geänderte Ausgangssituationen eine große Herausforderung dar. Des Weiteren ist die Software-Seite von Schwarmintelligenz weit fortgeschritten, allerdings scheitert es in der Praxis an den motorischen Fähigkeiten der Roboter.
Neben den technischen Aspekten von Schwarmintelligenz gibt es noch weitere Forschungsgebiete. Die Entscheidungsfindung innerhalb von Schwärmen kann einerseits die technische Umsetzung von Wahlen revolutionieren und andererseits unserer unserer Gesellschaft als Vorbild dienen. Schwärme treffen in der Regel wichtige Entscheidung in Echtzeit. Studien haben gezeigt, dass Wahlen, die in Echtzeit stattfinden, besser funktionieren. Allerdings hängt der Ausgang der Wahl davon ab, ob die Teilnehmer im Schwarm offen für neuen Input sind und das Gruppeninteresse über das Eigene ordnen.
Footnotes
-
Pietschmann, C. (2021, July 3). Vorbild Biologie. https://www.tagesspiegel.de/themen/freie-universitaet-berlin/forschung-zur-kuenstlichen-intelligenz-vorbild-biologie/27383616.html ↩
-
Beni, G. (2009). Swarm Intelligence. In R. A. Meyers (Ed.), Encyclopedia of Complexity and Systems Science (pp. 8869–8888). Springer New York. https://doi.org/10.1007/978-0-387-30440-3_530 ↩
-
Leibniz-Institut für Gewässerökologie und Binnenfischerei. Verhaltensbiologie und Schwarmintelligenz. Retrieved January 2, 2022, from https://www.igb-berlin.de/verhaltensbiologie-und-schwarmintelligenz ↩
-
Schmickl, T. (2009). Schwarmintelligenz am Beispiel der Ameisenstraßen. Denisia, 25, 141–155. https://www.zobodat.at/pdf/DENISIA_0025_0141-0155.pdf ↩ ↩2
-
Goss, S., Aron, S., Deneubourg, J.-L., & Pasteels, J. (1989). Self-organized shortcuts in the Argentine Ant. Naturwissenschaften 76: 579-581. Naturwissenschaften, 76, 579–581. https://doi.org/10.1007/BF00462870 ↩
-
Hamann, H. (2019). Szenarien. In Schwarmintelligenz (pp. 45–67). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-58961-8_3 ↩ ↩2
-
Bogon, T. (2013). Künstliche Intelligenz und Optimierung. In Agentenbasierte Schwarmintelligenz (pp. 11–38). Springer Fachmedien Wiesbaden. https://doi.org/10.1007/978-3-658-02292-1_2 ↩ ↩2
-
Dorigo, M., Birattari, M., & Stützle, T. (2006). Ant Colony Optimization. Computational Intelligence Magazine, IEEE, 1, 28–39. https://doi.org/10.1109/MCI.2006.329691 ↩
-
Bonabeau, E., Dorigo, M., & Theraulaz, G. (2001). Swarm Intelligence: From Natural to Artificial Systems / E. Bonabeau, M. Dorigo, G. Theraulaz. ↩
-
Tuba, M., & Jovanovic, R. (2009). An analysis of different variations of ant colony optimization to the minimum weight vertex cover problem. WSEAS Transactions on Information Science and Applications, 6. ↩
-
Thapar, P., & Batra, U. (2018). Implementation of Ant Colony Optimization in Routing Protocol for Internet of Things (pp. 151–164). https://doi.org/10.1007/978-981-10-4555-4_10 ↩
-
Sekaran, R., Kumar Munnangi, A., Rajeyyagari, S., Ramachandran, M., & Al-Turjman, F. (2021). Ant colony resource optimization for Industrial IoT and CPS. International Journal of Intelligent Systems. https://doi.org/https://doi.org/10.1002/int.22636 ↩
-
Kennedy, J., & Eberhart, R. (1995). Particle swarm optimization. Proceedings of ICNN’95 - International Conference on Neural Networks, 4, 1942–1948 vol.4. https://doi.org/10.1109/ICNN.1995.488968 ↩
-
Floreano, D., & Mattiussi, C. (2008). Bio-Inspired Artificial Intelligence: Theories, Methods, and Technologies. The MIT Press. ↩
-
Hamann, H. (2019). Modelle. In Schwarmintelligenz (pp. 69–92). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-58961-8_4 ↩
-
Holland, J. H. (1992). Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence. MIT Press. ↩
